Câu hỏi:
2 năm trước
Cho hình lăng trụ đứng $ABC.A'B'C'$ có $AB = 5cm,AC = 12cm,$$BC = 13cm.$ Có bao nhiêu mặt phẳng vuông góc với mặt phẳng $\left( {ABB'A'} \right)?$
Trả lời bởi giáo viên
Đáp án đúng: d
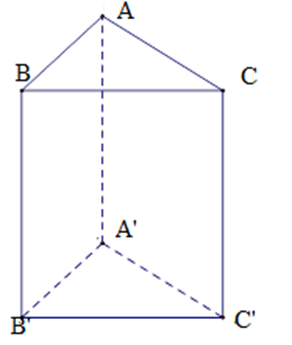
Tam giác $ABC$ có \(A{B^2} + A{C^2} = {5^2} + {12^2} = {13^2} = B{C^2}\) nên \(\Delta ABC\) vuông tại \(A\) (định lý Pytago đảo)
nên \(AC \bot AB\) . Do đó \(A'C' \bot A'B'\).
Vì $AC$ vuông góc với hai đường thẳng cắt nhau $AB$ và $AA'$ nên \(AC \bot mp(ABB'A')\)do đó \(mp(A'B'C') \bot mp(ABB'A')\).
Vậy có ba mặt phẳng vuông góc với mặt phẳng $\left( {ABB'A'} \right)$ là mp $\left( {ABC} \right)$ , mp $\left( {A'B'C'} \right),$ mp $\left( {ACC'A'} \right).$
Hướng dẫn giải:
+ Dùng định lý Pytago đảo để chứng minh tam giác vuông.
+ Dùng quan hệ vuông góc giữa hai mặt phẳng để tìm các cặp mặt phẳng vuông góc.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 8: hình lăng trụ đứng. hình chóp đều - đề số 1 Toán 8 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 8: hình lăng trụ đứng. hình chóp đều - đề số 2 Toán 8 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 8: hình lăng trụ đứng. hình chóp đều - đề số 1 Toán 8 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 8: hình lăng trụ đứng. hình chóp đều - đề số 2 Toán 8 có lời giải chi tiết
