Câu hỏi:
2 năm trước
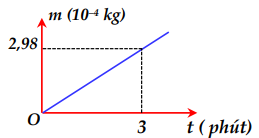
Một bình điện phân chứa dung dịch đồng sunphat \(\left( {CuS{O_4}} \right)\) với hai điện cực bằng đồng (Cu) . Người ta cho dòng điện không đổi có cường độ 5A chạy qua bình điện phân này rồi ghi lại độ tăng khối lượng của catốt theo thời gian. Đồ thị biểu diễn sự phụ thuộc của khối lượng catốt tăng lên theo thời gian được biểu diễn như hình bên. Đương lượng điện hóa của đồng (Cu) xác định được từ số liệu ở đồ thị trên là
Trả lời bởi giáo viên
Đáp án đúng: a
Khối lượng của chất giải phóng ở điện cực được tính bằng công thức:
\(m = \frac{1}{F}.\frac{A}{n}.It\)
Mà đương lượng điện hóa \(k = \frac{1}{F}.\frac{A}{n}\)
\(m = k.It \Rightarrow k = \frac{m}{{I.t}}\)
Từ đồ thị ta có: \(t = 3phut = 180s \Rightarrow m = 2,{98.10^{ - 4}}kg\)
\( \Rightarrow k = \frac{m}{{I.t}} = \frac{{2,{{98.10}^{ - 4}}}}{{5.180}} = 3,{31.10^{ - 7}}\left( {Kg/C} \right)\)
Hướng dẫn giải:
+ Định luật Faraday thứ nhất: Khối lượng vật chất được giải phóng ở điện cực của bình điện phân tỉ lệ thuận với điện lượng chạy qua bình: \(m = kq\)
+ Định luật Faraday thứ hai: Đương lượng điện hóa k của một nguyên tố tỉ lệ với đương lượng gam \(\frac{A}{n}\) của nguyên tố đó. Hệ số tỉ lệ là \(\frac{1}{F}\) , trong đó F gọi là hằng số Fa-ra-day: \(k = \frac{1}{F}.\frac{A}{n}\)
Kết hợp hai định luật: \(m = \frac{1}{F}.\frac{A}{n}.It\)
Câu hỏi khác
- Bài tập dòng điện trong chất điện phân - Phương pháp giải bài tập trong chất điện phân lý 11 có lời giải
- Bài tập dòng điện trong kim loại - Phương pháp giải bài tập dòng điện trong kim loại lý 11 có lời giải
- Bài tập dòng điện trong chất bán dẫn lý 11 có lời giải
- Bài tập dòng điện trong chất khí lý 11 có lời giải
- Bài tập dòng điện trong chân không lý 11 có lời giải
