Trả lời bởi giáo viên
Đáp án đúng: d
Điều kiện: \({x^3} - 3x > 0 \Leftrightarrow x\left( {{x^2} - 3} \right) > 0 \Leftrightarrow x\left( {x - \sqrt 3 } \right)\left( {x + \sqrt 3 } \right) > 0 \Leftrightarrow \left[ \begin{array}{l} - \sqrt 3 < x < 0\\x > \sqrt 3 \end{array} \right..\)
Ta có: \(y' = e\left( {3{x^2} - 3} \right){\left( {{x^3} - 3x} \right)^{e - 1}}.\)
\( \Rightarrow y' = 0 \Leftrightarrow \left( {3{x^2} - 3} \right){\left( {{x^3} - 3x} \right)^{e - 1}} = 0 \Leftrightarrow 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\end{array} \right.\)
Ta có bảng xét dấu:
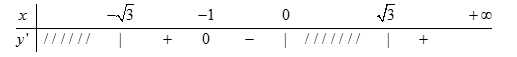
Dựa vào bảng xét dấu của hàm số ta thấy đạo hàm của hàm số chỉ đổi dấu qua 1 điểm \(x = - 1 \Rightarrow \) hàm số có 1 điểm cực trị.
Hướng dẫn giải:
Ta có: \(x = {x_0}\) là điểm cực trị của hàm số \(y = f\left( x \right) \Rightarrow f'\left( {{x_0}} \right) = 0.\)
Câu hỏi khác
- Đề thi thử THPTQG môn Toán Chuyên ĐH Vinh Nghệ An lần 3 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 1 Toán 12 có lời giải chi tiết
- Đề tập huấn thi THPTQG Sở Giáo Dục và Đào Tạo Bắc Ninh 2019 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 4 Toán 12 có lời giải chi tiết
