Câu hỏi:
3 năm trước
Hai hình bình hành $ABCD$ và $ABEF$ không cùng nằm trong một mặt phẳng. Gọi $O$ và $O’$ lần lượt là tâm hình bình hành $ABCD $ và $ABEF.$ $OO’$ song song với:
Trả lời bởi giáo viên
Đáp án đúng: d
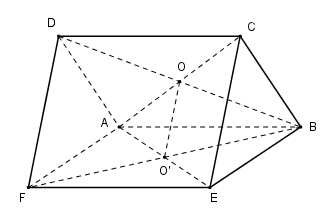
Vì $O$ và $O’$ lần lượt là tâm hình bình hành $ABCD $ và $ABEF$ nên $O$ là trung điểm của $BD;$ $O’$ là trung điểm của $FB.$
Xét tam giác $BDF $ có: $OO’$ là đường trung bình \( \Rightarrow \) $OO’ // DF$
Mà \(DF \subset \left( {DCEF} \right);\) \(DF \subset \left( {ADF} \right)\,;\) \(\,DF // \left( {BCE} \right)\)
Nên $OO’ // (DCEF) ;$ $ OO’ // (ADF) ;$ $ OO’ // (BCE)$ (cùng song song với DF).
Hướng dẫn giải:
- Sử dụng tính chất của tâm hình bình hành.
- Áp dụng định lí Ta – let đảo để chứng minh các đường thẳng song song.