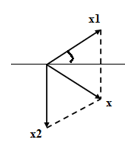
Hai dao động cùng phương lần lượt có phương trình ${x_1} = {A_1}{\rm{cos(}}\pi {\rm{t + }}\frac{\pi }{6})(cm)$ và ${x_2} = 6{\rm{cos(}}\pi {\rm{t - }}\frac{\pi }{2})(cm)$. Dao động tổng hợp của hai dao động này có phương trình $x = A{\rm{cos(}}\pi {\rm{t + }}\varphi$ (cm). Thay đổi A₁ cho đến khi A đạt giá trị cực tiểu thì:

Biên độ dao động:

Một con lắc lò xo dao động theo phương ngang với cơ năng dao động là \(32mJ\) và lực đàn hồi cực đại tác dụng lên vật có độ lớn là \(4N\). Biên độ dao động của con lắc là:

Trong các phương trình sau phương trình nào không biểu thị cho dao động điều hòa ?

Một con lắc đơn dao động với phương trình \(s = 2\cos 2\pi t\left( {cm} \right)\) (t tính bằng giây). Tần số dao động của con lắc là

Một vật dao động điều hòa theo phương trình \(x = 5cos\left( {\pi t} \right)cm\). Gia tốc cực đại của vật bằng:

Tại một điểm trên mặt chất lỏng có một nguồn dao động với tần số $120 Hz$, tạo ra sóng ổn định trên mặt chất lỏng. Xét $5$ gợn lồi liên tiếp trên một phương truyền sóng ở về một phía so với nguồn, gợn thứ nhất cách gợn thứ năm $0,5m$. Tính tốc độ truyền sóng trên mặt chất lỏng:

Một đồng hồ quả lắc được coi như một con lắc đơn chạy đúng giờ tại một địa điểm trên mặt đất. Khi nhiệt độ môi trường giảm thì đồng hồ