Gọi $(H)$ là phần giao của hai khối $\dfrac{1}{4}$ hình trụ có bán kính $a$, hai trục hình trụ vuông góc với nhau như hình vẽ bên.
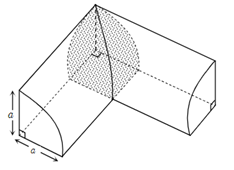
Tính thể tích của $(H)$.
Trả lời bởi giáo viên
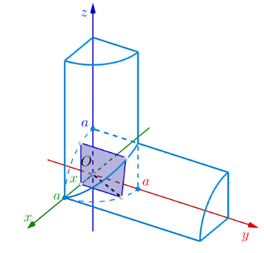
Gọi trục tọa độ $Oxyz$ như hình vẽ.
Khi đó phần giao (H) là một vật thể có đáy là một phần tư hình tròn tâm O bán kính a, thiết diện của mặt phẳng vuông góc với trục Ox là một hình vuông có diện tích \(S\left( x \right) = {a^2} - {x^2}\)
Thể tích khối (H) là \(\int\limits_0^a {S\left( x \right)dx = } \int\limits_0^a {\left( {{a^2} - {x^2}} \right)dx} = \dfrac{{2{a^3}}}{3}\)
Hướng dẫn giải:
- Gắn hệ trục tọa độ $Oxyz$.
- Khi đó phần giao (H) là một vật thể có đáy là một phần tư hình tròn tâm O bán kính a, thiết diện của mặt phẳng vuông góc với trục Ox là một hình vuông có diện tích \(S\left( x \right) = {a^2} - {x^2}\).


