Xét hàm số \(y = \sin \,x\) trên đoạn \(\left[ { - \pi ;\,0} \right].\) Khẳng định nào sau đây là đúng?
Trả lời bởi giáo viên
Từ bảng biến thiên của hàm số $y=\sin x$ trên $[-\pi ; \pi]$ ta có hàm số \(y = \sin x\) nghịch biến trên khoảng \(\left( { - \pi ;\, - \dfrac{\pi }{2}} \right)\) và đồng biến trên khoảng \(\,\,\left( { - \dfrac{\pi }{2};\,0} \right).\)
Hướng dẫn giải:
Bảng biến thiên của hàm số \(y = \sin x\) trên \(\left[ { - \pi ;\pi } \right]\)
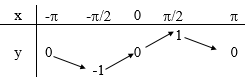
Giải thích thêm:
Cách 2: Sử dụng máy tính cầm tay.
Do ở đề bài, các phương án A, B, C, D chỉ xuất hiện hai khoảng là \(\left( { - \pi ;\, - \dfrac{\pi }{2}} \right)\)và \(\,\,\left( { - \dfrac{\pi }{2};\,0} \right)\) nên ta sẽ dùng máy tính cầm tay chức năng MODE 7: TABLE để giải bài toán.
Ấn MODE 7
Máy hiện \(f\left( X \right) = \) thì ta nhập \(\sin {\rm{X}}\). START? Nhập \( - \pi ;\,\)END? Nhập \(0.\) STEP? Nhập \(\dfrac{\pi }{{10}}.\)

Lúc này từ bảng giá trị của hàm số ta thấy hàm số nghịch biến trên khoảng \(\left( { - \pi ;\, - \dfrac{\pi }{2}} \right)\)và đồng biến trên khoảng\(\,\,\left( { - \dfrac{\pi }{2};\,0} \right).\)

