Trả lời bởi giáo viên
Theo đề bài ta có: R1 = R2 = R3 = R
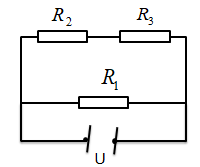
\({R_2}\,nt\,{R_3} \Rightarrow {R_{23}} = {R_2} + {R_3} = 2R\)
\(\left[ {{R_2}\,nt\,{R_3}} \right]//{R_1} \Rightarrow {U_1} = {U_{23}} = U\)
\( \Rightarrow {I_{23}} = \frac{{{U_{23}}}}{{{R_{23}}}} = \frac{U}{{2{\rm{R}}}}\)
Công suất tiêu thụ trên \({R_1}\) là: \({P_1} = \frac{{{U^2}}}{{{R_1}}} = \frac{{{U^2}}}{R}\)
Công suất tiêu thụ trên \({R_2},{R_3}\) là:
\({P_2} = {P_3} = I_2^2.{R_2} = I_3^2.{R_3} = \left( {\frac{{{U^2}}}{{2{\rm{R}}}}} \right).R = \frac{{{U^2}}}{{4{\rm{R}}}}\)
\( \Rightarrow {P_{23}} = {P_2} + {P_3} = \frac{{{U^2}}}{{4{\rm{R}}}} + \frac{{{U^2}}}{{4{\rm{R}}}} = \frac{{{U^2}}}{{{\rm{2R}}}} < {P_1}\)
Vậy công suất lớn nhất ở \({R_1}\).
Hướng dẫn giải:
Sử dụng công thức tính công suất: \(P = {I^2}R = \frac{{{U^2}}}{R}\)