Câu hỏi:
2 năm trước
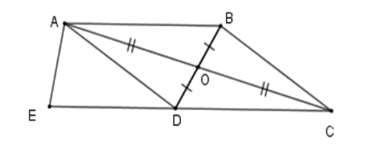
Cho tứ giác $ABCD$ . Gọi$E$ , $F$ lần lượt là giao điểm của $AB$ và $CD$ , $AD$ và $BC;$ $M,N,P,Q$ lần lượt là trung điểm của $AE$ , $EC$ , $CF$ ,$FA$ . Khi đó \(MNPQ\) là hình gì? Chọn đáp án đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: a
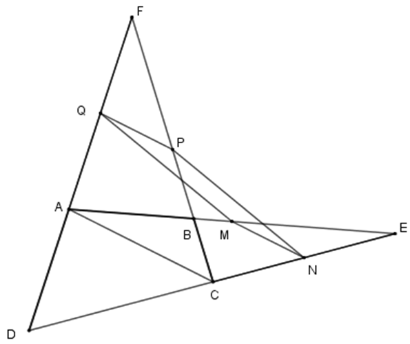
Nối \(AC\) .Vì $M,N$ lần lượt là trung điểm của$AE$ , $EC$ nên \(MN\) là đườn gtrung bình của tam giác \(EAC\) suy ra \(MN{\rm{//}}AC;\,MN = \dfrac{1}{2}AC\) $\left( 1 \right)$ .
Tương tự \(PQ\) là đường trung bình của tam giác \(FAC\) suy ra \(PQ{\rm{//}}AC;\,PQ = \dfrac{1}{2}AC\) \(\left( 2 \right)\) .
Từ \(\left( 1 \right);\,\left( 2 \right)\) suy ra \(PQ{\rm{//}}NM;\,PQ = MN\) nên \(MNPQ\) là hình bình hành (dhnb).
Hướng dẫn giải:
Bước 1: Sử dụng tính chất đường trung bình của tam giác để chứng minh các cạnh song song và bằng nhau.
Bước 2: Sử dụng dấu hiệu nhận biết để suy ra \(MNPQ\) là hình bình hành.
