Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) đều, cạnh \(2cm\); \(M,N\) là trung điểm của \(AB\) và \(AC\). Chu vi của tứ giác \(MNCB\) bằng
Trả lời bởi giáo viên
Đáp án đúng: a
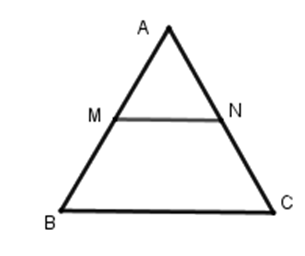
+ \(M,N\) là trung điểm của \(AB\) và \(AC\)nên \(MN\) là đường trung bình của tam giác \(ABC\) \( \Rightarrow MN = \dfrac{1}{2}BC = \dfrac{1}{2}.2 = 1\,cm\) .
+ \(MB = \dfrac{{AB}}{2} = \dfrac{2}{2} = 1\,cm;\,NC = \dfrac{{AC}}{2} = \dfrac{2}{2} = 1\,cm\)
+ Chu vi tứ giác \(MNCB\) là \(P = MN + BC + MB + NC\)\( = 1 + 1 + 1 + 2 = 5\,cm\) .
Hướng dẫn giải:
Bước 1: Ta sử dụng định lý đường trung bình của hình thang để tính độ dài cạnh \(MN\) .
Bước 2: Chu vi tứ giác \(MNCB\) là \(P = MN + BC + MB + NC\) .