Câu hỏi:
2 năm trước
Cho tứ giác $ABCD.$ Gọi $E,F,G,H$ theo thứ tự là trung điểm của $AB,BC,CD,DA$ . Tìm điều kiện của tứ giác $ABCD$ để hình bình hành $EFGH$ là hình vuông.
Trả lời bởi giáo viên
Đáp án đúng: a
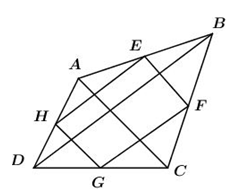
Ta có \(EH;\,EF\) lần lượt là đường trung bình của tam giác \(ABD;\,BAC\) nên
\(\left\{ \begin{array}{l}EH//BD;\,\,\,EF//AC\\EH = \dfrac{1}{2}BD;\,\,EF = \dfrac{1}{2}AC\end{array} \right.\,\,\left( 1 \right)\)
Hình bình hành EFGH là hình vuông khi và chỉ khi\(\left\{ \begin{array}{l}EH \bot EF\\EH = EF\end{array} \right.\,\left( 2 \right)\)
Từ \(\left( 1 \right);\,\left( 2 \right) \Rightarrow \left\{ \begin{array}{l}BD \bot AC\\DB = AC\end{array} \right.\) thì hình bình hành $EFGH$ là hình vuông.
Hướng dẫn giải:
Dựa vào hai dấu hiệu nhận biết:
+ Hình bình hành có một góc vuông là hình chữ nhật
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
