Cho tứ diện đều $SABC.$ Gọi $I$ là trung điểm của $AB, M $ là một điểm di động trên đoạn $AI.$ Gọi $(P)$ là mặt phẳng qua $M$ và song song với $SI, IC,$ biết $AM = x.$ Thiết diện tạo bởi $mp(P)$ và tứ diện $SABC $ có chu vi là:

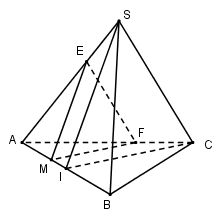
Trong $mp(ABC)$ kẻ $MF // IC$ \(\left( {F \in AC} \right)\), trong $mp(SAB)$ kẻ $ME // SI$ \(\left( {E \in SA} \right)\).

Do đó $mp(P)$ chính là $(MEF)$ và thiết diện tạo bởi $mp(P)$ và tứ diện đều $SABC$ là tam giác $MEF.$

Gọi $a$ là cạnh của tứ diện đều $SABC.$

Xét tam giác đều $ABC$ và tam giác $SAB$ là những tam giác đều cạnh $a$ nên \(CI = SI = \dfrac{{a\sqrt 3 }}{2}\).

Trong $(ABC)$ ta có: \(\dfrac{{AM}}{{AI}} = \dfrac{{ME}}{{SI}} \Leftrightarrow \dfrac{x}{{\dfrac{a}{2}}} = \dfrac{{ME}}{{\dfrac{{a\sqrt 3 }}{2}}} \Leftrightarrow ME = x\sqrt 3 .\)

Trong $(SAB)$ ta có: \(\dfrac{{AM}}{{AI}} = \dfrac{{MF}}{{CI}} \Leftrightarrow \dfrac{x}{{\dfrac{a}{2}}} = \dfrac{{MF}}{{\dfrac{{a\sqrt 3 }}{2}}} \Leftrightarrow MF = x\sqrt 3 .\)

Ta lại có: \(\dfrac{{AM}}{{AI}} = \dfrac{{AF}}{{AC}} = \dfrac{{AE}}{{AS}} \) \(\Rightarrow EF\) $// SC $ (Định lí Ta-let đảo)

\( \Rightarrow \dfrac{{EF}}{{SC}} = \dfrac{{AF}}{{AC}} = \dfrac{{AM}}{{AI}} \Leftrightarrow \dfrac{{EF}}{a} = \dfrac{x}{{\dfrac{a}{2}}} \Leftrightarrow EF = 2x\)

Vậy chu vi tam giác $MEF $ bằng $ME + MF + EF =$ \(x\sqrt 3  + x\sqrt 3  + 2x = 2x\left( {1 + \sqrt 3 } \right)\)