Cho tứ diện đều \(ABCD\) có tam giác \(BCD\) đều,\(AD = AC\). Giá tri của \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right)\)là:
Trả lời bởi giáo viên
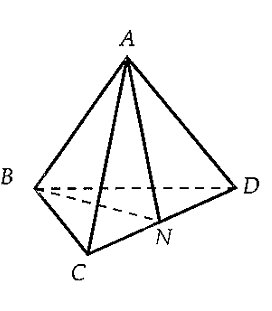
Gọi \(N\) là trung điểm của \(CD\). Tam giác đều \(BCD\) nên \(BN \bot CD\). Tam giác \(ACD\)cân tại \(A\) nên \(AN \bot CD\) ta có:
$\overrightarrow {AB} .\overrightarrow {CD} = \left( {\overrightarrow {AN} + \overrightarrow {NB} } \right).\overrightarrow {CD} = \overrightarrow {AN} .\overrightarrow {CD} + \overrightarrow {NB} .\overrightarrow {CD} = 0 \Rightarrow c{\rm{os}}\left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {CD} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}} = 0$
Hướng dẫn giải:
Sử dụng công thức tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \dfrac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\).
Giải thích thêm:
Các em cũng có thể chứng minh \(CD \bot \left( {ABN} \right) \Rightarrow CD \bot AB\) sẽ học ở bài sau.

