Câu hỏi:
2 năm trước
Cho tứ diện đều $ABCD$ có cạnh bằng $8$. Ở bốn đỉnh tứ diện, người ta cắt đi các tứ diện đều bằng nhau có cạnh bằng $x$, biết khối đa diện tạo thành sau khi cắt có thể tích bằng \(\dfrac{3}{4}\) thể tích tứ diện $ABCD$. Giá trị của $x$ là:
Trả lời bởi giáo viên
Đáp án đúng: d
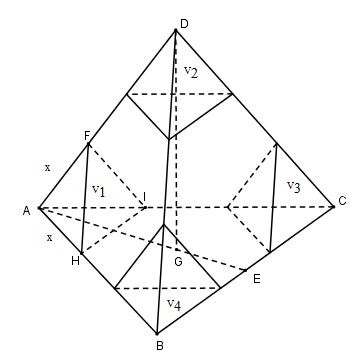
Tứ diện \(ABCD\) đều cạnh \(a\) có thể tích là \({V_{ABCD}} = \dfrac{{{a^3}\sqrt 2 }}{{12}}\)
Vì tứ diện đều $ABCD$ cạnh $8$ nên \({V_{ABCD}} = \dfrac{{{8^3}\sqrt 2 }}{{12}} = \dfrac{{128\sqrt 2 }}{3}\)
Tứ diện đều $FAHI$ cạnh $x$ nên \({V_1} = \dfrac{{{x^3}\sqrt 2 }}{{12}}\)
Tương tự ta có: \({V_2} = {V_3} = {V_4} = \dfrac{{{x^3}\sqrt 2 }}{{12}}\)
\( \Rightarrow \)Khối đa diện tạo thành sau khi cắt có thể tích là \(V = {V_{ABCD}} - 4{V_1} = \dfrac{{128\sqrt 2 }}{3} - 4\dfrac{{{x^3}\sqrt 2 }}{{12}} = \dfrac{{\left( {128 - {x^3}} \right)\sqrt 2 }}{3}\)
Vì khối đa diện tạo thành sau khi cắt có thể tích bằng \(\dfrac{3}{4}\) thể tích tứ diện $ABCD$ nên ta có:
\(\dfrac{{\left( {128 - {x^3}} \right)\sqrt 2 }}{3} = \dfrac{3}{4}\dfrac{{128\sqrt 2 }}{3} \Rightarrow 128 - {x^3} = 96 \Leftrightarrow {x^3} = 32 \Rightarrow x = \sqrt[3]{{32}} = 2\sqrt[3]{4}\)
Hướng dẫn giải:
Sử dụng công thức tính thể tích khối tứ diện đều cạnh \(a:V = \dfrac{{{a^3}\sqrt 2 }}{{12}}\) để tính thể tích các khối tứ diện đều trong bài.
