Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang vuông tại \(A\) và \(D\) thỏa mãn \(SA \bot \left( {ABCD} \right)\) và \(AB = 2AD = 2CD = 2a = \sqrt 2 SA\). Thể tích khối chóp \(S.BCD\) là:
Trả lời bởi giáo viên
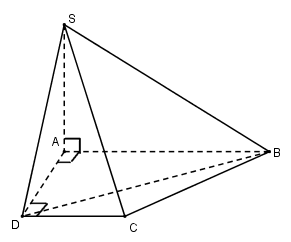
Ta có: \({S_{ABCD}} = \dfrac{1}{2}\left( {AB + CD} \right).AD = \dfrac{1}{2}\left( {2a + a} \right)a = \dfrac{{3{a^2}}}{2}\)
\({S_{\Delta ABD}} = \dfrac{1}{2}AD.AB = \dfrac{1}{2}a.2a = {a^2}\)
\( \Rightarrow {S_{BCD}} = {S_{ABCD}} - {S_{ABD}} = \dfrac{{3{a^2}}}{2} - {a^2} = \dfrac{{{a^2}}}{2}\)
\(SA = \dfrac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \)
\( \Rightarrow {V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
Hướng dẫn giải:
- Bước 1: Tính diện tích đáy \({S_{\Delta BCD}}\), dựa vào các tính chất của đáy.
- Bước 2: Tính chiều cao \(h = SA\).
- Bước 3: Tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\).
Giải thích thêm:
Một số em sẽ tính nhầm \(SA = \dfrac{{a\sqrt 2 }}{2}\) dẫn đến chọn nhầm đáp án D là sai.

