Cho tứ diện đều $ABCD$ có cạnh $a$. Một mặt cầu tiếp xúc với các mặt của tứ diện có bán kính là:

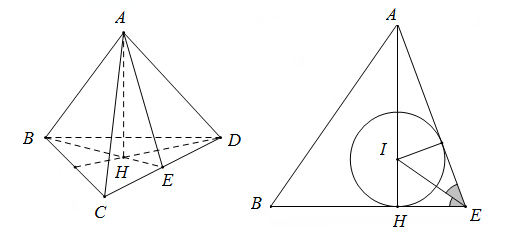
Gọi $H$ là tâm tam giác đều $BCD,E$ là trung điểm $CD$

Ta có $AH \bot \left( {BCD} \right)$

Gọi $I,r$ là tâm và bán kính mặt cầu tiếp xúc với các mặt của tứ diện $ABCD$ thì $I$ là giao của $AH$ và phân giác góc $AEB$ của $\Delta AEB$. Ta có

$\begin{array}{l}AE = BE = \dfrac{{a\sqrt 3 }}{2};HE = \dfrac{{BE}}{3} = \dfrac{{a\sqrt 3 }}{6}\\AH = \sqrt {A{E^2} - H{E^2}}  = \dfrac{{a\sqrt 6 }}{3}\end{array}$

Áp dụng tính chất đường phân giác:

$\begin{array}{l}\dfrac{{IH}}{{IA}} = \dfrac{{EH}}{{EA}} \Rightarrow \dfrac{{IH}}{{IH + IA}} = \dfrac{{EH}}{{EH + EA}}\\ \Rightarrow r = IH = \dfrac{{EH.AH}}{{EH + EA}} = \dfrac{{a\sqrt 6 }}{{12}}\end{array}$