Câu hỏi:
3 năm trước
Cho tứ diện $ABCD,$ gọi $G$ là trọng tâm tam giác $ACD,$ $M$ thuộc đoạn thẳng $BC$ sao cho $CM = 2MB.$ Chọn mệnh đề đúng trong các mệnh đề sau?
Trả lời bởi giáo viên
Đáp án đúng: b
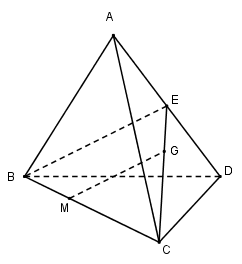
Gọi $E$ là trung điểm của $AD$ ta có \(G \in CE\) và \(\dfrac{{CG}}{{CE}} = \dfrac{2}{3}\)
Vì \(CM = 2MB \Rightarrow \dfrac{{CM}}{{CB}} = \dfrac{2}{3}\)
Xét tam giác $BCE$ có: \(\dfrac{{CG}}{{CE}} = \dfrac{{CM}}{{CB}} = \dfrac{2}{3} \)
\(\Rightarrow \) $MG // BE$ (Định lí Ta – let đảo)
Mà \(BE \subset \left( {ABD} \right)\) \( \Rightarrow \) $MG // (ABD)$
Hướng dẫn giải:
- Đưa về cùng một mặt phẳng.
- Sử dụng tính chất trọng tâm của tam giác.
- Áp dụng định lí Ta – let đảo để chứng minh hai đường thẳng song song.