Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) có \(\widehat C > \widehat B\) (\(\widehat B,\,\widehat C\) là các góc nhọn). Vẽ phân giác \(AD.\) So sánh \(BD\) và \(CD.\)
Trả lời bởi giáo viên
Đáp án đúng: d
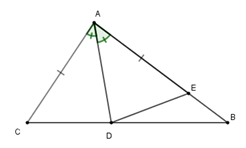
Từ đề bài \(\widehat C > \widehat B \Rightarrow AB > AC.\) Trên cạnh \(AB\) lấy điểm \(E\) sao cho \(AC = AE.\)
Xét tam giác \(ACD\) và tam giác \(AED\) có
+ \(AC = AE\)
+ \(\widehat {CAD} = \widehat {DAB}\) (tính chất tia phân giác)
+ Cạnh \(AD\) chung
Suy ra \(\Delta ACD = \Delta AED\left( {c - g - c} \right)\)
\( \Rightarrow DE = CD\,\,\left( 1 \right)\) và \(\widehat {AED} = \widehat {ACD}\)
Mà \(\widehat {ACD}\) là góc nhọn nên \(\widehat {AED}\) là góc nhọn, suy ra \(\widehat {BED} = 180^\circ - \widehat {AED}\) là góc tù, do đó \(\widehat {BED} > \widehat {EBD}\)
Xét tam giác \(BED\) có \(\widehat {BED} > \widehat {EBD}\) suy ra \(BD > DE\,\,\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(DC < BD.\)
Hướng dẫn giải:
+ Trên cạnh \(AB\) lấy điểm \(E\) sao cho \(AC = AE.\)
+ So sánh $CD$ với \(DE\) bằng cách sử dụng hai tam giác bằng nhau
+ So sánh $DE$ với \(BC\) theo quan hệ giữa cạnh và góc trong tam giác
+ Từ đó so sánh \(CD\) và \(BD.\)
Câu hỏi khác
- Đề kiểm tra 15 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 2 Toán 7 có lời giải chi tiết
