Câu hỏi:
2 năm trước
Cho tam giác $ABC$ có $\widehat B = {60^0},\widehat C = {50^0},AC = 3,5cm.$ Diện tích tam giác $ABC$ gần nhất với giá trị nào dưới đây?
Trả lời bởi giáo viên
Đáp án đúng: b
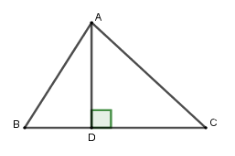
Kẻ đường cao \(AD\).
Xét tam giác vuông \(ACD\), có $AD = AC.\sin C = 3,5.\sin 50^\circ \approx 2,68\,cm$; $CD = AC.\cos C = 3,5.\cos 50^\circ \approx 2,25\,\,cm$
Xét tam giác vuông \(ABD\), có $BD = AD.\cot B \approx 2,68.\cot 60^\circ \approx 1,55\,\,cm$
Suy ra $BC = BD + CD = 3,8$
Do đó ${S_{ABC}} = \dfrac{{AD.BC}}{2} \approx 5,09$$c{m^2}$.
Hướng dẫn giải:
+) Kẻ đường cao $AD$
+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông thích hợp và định lý Py-ta-go để tính cạnh.
+) Sử dụng công thức tính diện tích tam giác.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 5: hệ thức lượng trong tam giác vuông - đề số 1 Toán 9 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 5: hệ thức lượng trong tam giác vuông - đề số 2 Toán 9 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 5: hệ thức lượng trong tam giác vuông - đề số 1 Toán 9 có lời giải chi tiết
