Câu hỏi:
2 năm trước
Cho ${q_1} = {\rm{ }}{4.10^{ - 10}}C,{\rm{ }}{q_2} = {\rm{ }} - 4.{\rm{ }}{10^{ - 10}}C$, đặt tại A và B trong ko khí biết $AB{\rm{ }} = {\rm{ }}2{\rm{ }}cm$. Xác định vectơ $\vec E$tại điểm $M$, biết $MA{\rm{ }} = {\rm{ }}1{\rm{ }}cm,{\rm{ }}MB{\rm{ }} = {\rm{ }}3{\rm{ }}cm$.
Trả lời bởi giáo viên
Đáp án đúng: b
- Gọi cường độ điện trường do ${q_1}$ gây ra là ${E_1}$ ; do ${q_2}$ gây ra là ${E_2}$
- Theo nguyên lí chồng chất điện trường:$\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} $
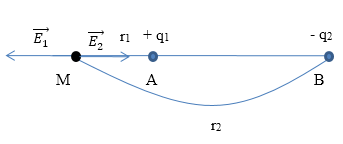
Vì ${E_1},{\rm{ }}{E_2}$ là 2 véc tơ cùng phương, ngược chiều nên: $E{\rm{ }} = {\rm{ }}{E_1} - {\rm{ }}{E_2}$
Ta có, cường độ điện trường: $E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}$
Thay ${q_1} = {\rm{ }}{4.10^{ - 10}}C,{\rm{ }}{q_2} = {\rm{ }} - {4.10^{ - 10}}C,{\rm{ }}{r_1} = {\rm{ }}1cm{\rm{ }},{r_2} = {\rm{ }}3cm,\varepsilon = 1$
Ta có:
${E_1} = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r_1}^2}} = {9.10^9}\dfrac{{\left| {{{4.10}^{ - 10}}} \right|}}{{1.0,{{01}^2}}} = {36.10^3}V/m$
${E_2} = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r_2}^2}} = {9.10^9}\dfrac{{\left| {{{4.10}^{ - 10}}} \right|}}{{1.0,{{03}^2}}} = {4.10^3}V/m$
$ = > E{\rm{ }} = {\rm{ }}{E_1} - {\rm{ }}{E_2} = 32.{\rm{ }}{10^3}V/m$
Hướng dẫn giải:
+ Áp dụng nguyên lí chồng chất điện trường: $\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} $
+ Áp dụng biểu thức xác định cường độ điện trường: $E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}$
Câu hỏi khác
- Bài tập từ trường tự chọn ĐGTD ĐHBK HN có lời giải
- Bài tập dòng điện không đổi tự chọn ĐGTD ĐHBK HN có lời giải
- Bài tập điện trường tự chọn ĐGTD ĐHBK HN có lời giải
- Bài tập điện năng - công suất điện tự chọn ĐGTD ĐHBK HN có lời giải
- Bài tập sự nhiễm điện - điện tích. định luật culông tự chọn ĐGTD ĐHBK HN có lời giải
