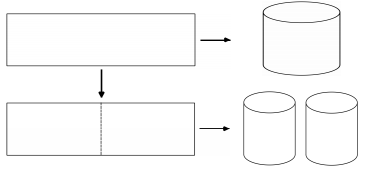
Cho lăng trụ tam giác đều ABC.A’B’C’ có thể tích bằng 1. Gọi (T) là hình trụ nội tiếp lăng trụ và M là tâm của mặt bên BCC’B’. Mặt phẳng (P) chứa AM cắt hình trụ (T) như hình vẽ.
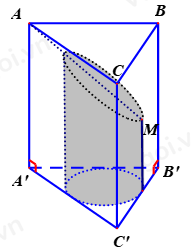
Thể tích khối hình còn lại (phần tô đậm) của khối trụ (T) là
Trả lời bởi giáo viên
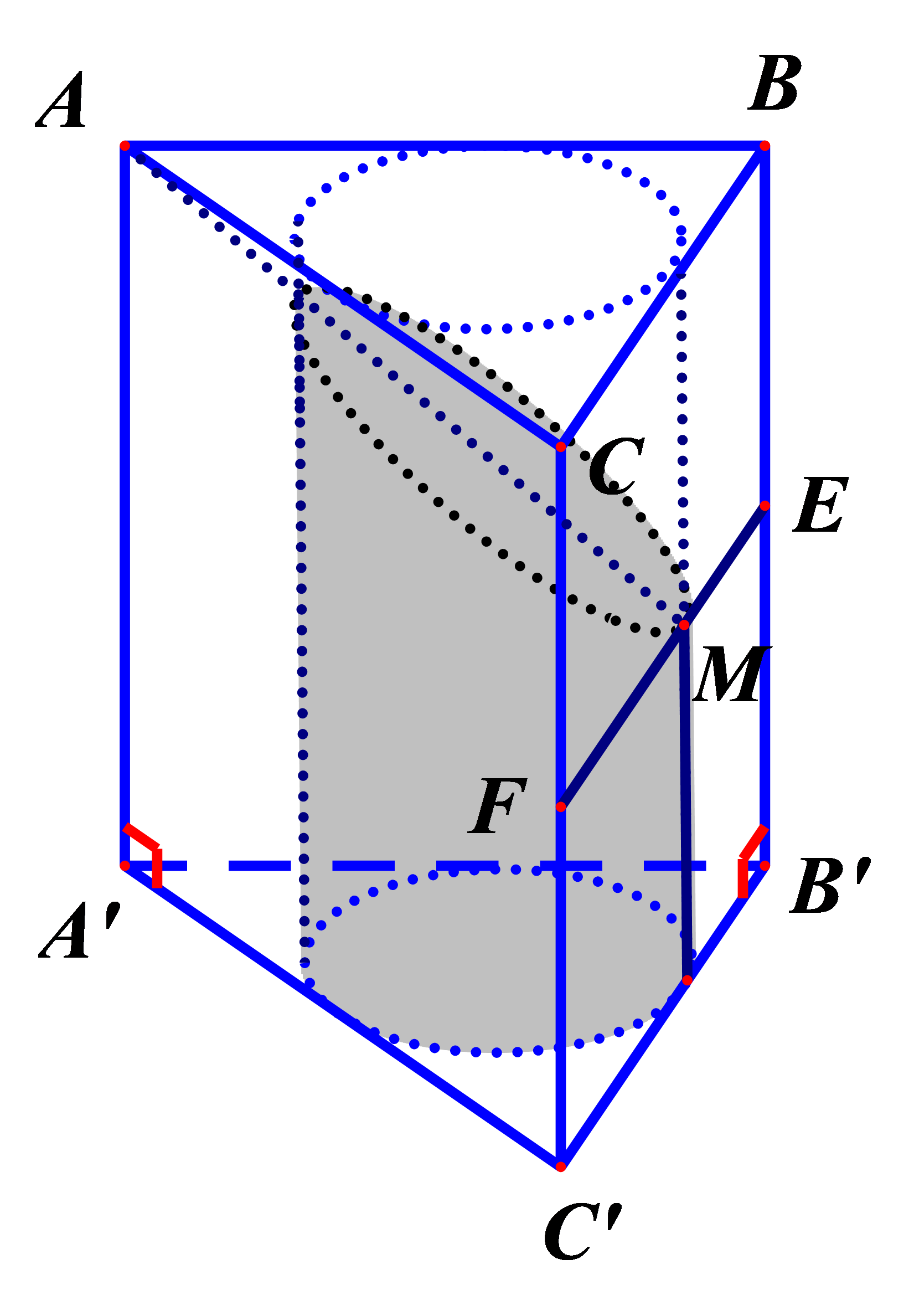
Giả sử h=S=1
Cạnh AB=a, bán kính đường tròn nội tiếp tam giác A’B’C’ là r và p là nửa chu vi của tam giác ABC.
Khi đó ta có: S=p.r=1
Mà
\(\begin{array}{l}p = \dfrac{{3a}}{2};S = \sqrt {p{{\left( {p - a} \right)}^3}} = 1\\ \Rightarrow p{\left( {p - a} \right)^3} = 1 \Leftrightarrow \dfrac{{3a}}{2}{\left( {\dfrac{a}{2}} \right)^3} = 1\\ \Leftrightarrow a = \dfrac{2}{{\sqrt[4]{3}}} \Rightarrow p = \sqrt[4]{{27}} \Rightarrow r = \dfrac{1}{{\sqrt[4]{{27}}}}\\\dfrac{{{V_{tru}}}}{{{V_{ltru}}}} = \dfrac{{{S_{tron}}}}{{{S_{A'B'C'}}}} = \dfrac{{\pi {r^2}}}{{pr}} = \dfrac{{\pi r}}{p} = \dfrac{{\pi .1}}{{\sqrt {27} }}\\ \Rightarrow {V_{tru}} = \dfrac{\pi }{{\sqrt {27} }}\end{array}\)
Gọi thể tích của khối trụ bị cắt bỏ là \({V_1}\) và phần tô đậm của (T) là \({V_2}\)
Mà thiết diện khi lăng trụ bị cắt là tam giác AEF với E và F lần lượt là trung điểm của BB’ và CC’
Khi đó \(\dfrac{{{V_{ABCFE}}}}{{V _{ABC.A'B'C'}}} = \dfrac{{{V_1}}}{{{V_1} + {V_2}}}\)
Ta có:
\(\begin{array}{l}\dfrac{{{V_{ABCFE}}}}{{V _{ABC.A'B'C'}}} = \dfrac{{0 + \dfrac{1}{2} + \dfrac{1}{2}}}{3} = \dfrac{1}{3}\\ \Rightarrow \dfrac{{{V_1}}}{{{V_1} + {V_2}}} = \dfrac{1}{3} \Rightarrow \dfrac{{{V_2}}}{{{V_1} + {V_2}}} = \dfrac{2}{3}\\ \Rightarrow {V_2} = \dfrac{2}{3}.{V_{tru}} = \dfrac{2}{3}.\dfrac{\pi }{{\sqrt {27} }} = \dfrac{{2\pi \sqrt 3 }}{{27}}\end{array}\)
Hướng dẫn giải:
- Giả sử h=S=1
- Tính thể tích của khối lăng trụ
- Gọi thể tích của khối trụ bị cắt bỏ là \({V_1}\) và khối trụ (T) là \({V_2}\)
- Khi cắt lăng trụ bởi một mặt phẳng thì tỷ lệ thể tích khối trụ nội tiếp và thể tích lăng trụ được bảo toàn.