Câu hỏi:
2 năm trước
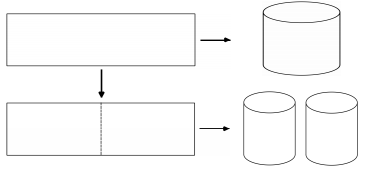
Từ một tấm tôn hình chữ nhật kích thước $50cm \times 240cm$, người ta làm các thùng đựng nước hình trụ có chiều cao bằng $50cm$, theo hai cách sau (xem hình minh họa dưới đây):
- Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
- Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu ${V_1}$ là thể tích của thùng gò được theo cách 1 và ${V_2}$ là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số $\dfrac{{{V_1}}}{{{V_2}}}$.
Trả lời bởi giáo viên
Đáp án đúng: c
Cách 1: Chu vi đáy là $240cm \Rightarrow 2\pi {R_1} = 240 \Leftrightarrow {R_1} = \dfrac{{120}}{\pi } $
$\Rightarrow {V_1} = \pi R_1^2h = \pi {\left( {\dfrac{{120}}{\pi }} \right)^2}h = \dfrac{{{{120}^2}.50}}{\pi }$
Cách 2: Chu vi đáy mỗi hình trụ nhỏ là:
\(240:2 = 120cm \Rightarrow 2\pi R = 120 \Rightarrow R = \dfrac{{60}}{\pi } \)
$\Rightarrow V = \pi {R^2}h = \pi {\left( {\dfrac{{60}}{\pi }} \right)^2}.50 = \dfrac{{{{60}^2}.50}}{\pi } \Rightarrow {V_2} = 2V = \dfrac{{{{2.60}^2}.50}}{\pi }$
Vậy \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{{{120}^2}.50}}{\pi }:\dfrac{{{{2.60}^2}.50}}{\pi } = 2\)
Một đường tròn có bán kính $r$ thì có chu vi và diện tích lần lượt là $C = 2\pi r;S = \pi {r^2} \Rightarrow S = \dfrac{{{C^2}}}{{4\pi }}$
Gọi chiều dài tấm tôn là $a$ thì tổng diện tích đáy của thùng theo 2 cách lần lượt là
${S_1} = \dfrac{{{a^2}}}{{4\pi }};{S_2} = 2.\dfrac{{{{\left( {\dfrac{a}{2}} \right)}^2}}}{{4\pi }} = \dfrac{{{a^2}}}{{8\pi }} \Rightarrow \dfrac{{{S_1}}}{{{S_2}}} = 2 \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = 2$
Hướng dẫn giải:
- Tính bán kính mỗi khối trụ trong từng trường hợp, sử dụng công thức chu vi \(C = 2\pi R\).
- Tính thể tích mỗi khối trụ trong từng trường hợp, sử dụng công thức \(V = \pi {R^2}h\).
- Từ đó suy ra tỉ số cần tìm.
