Cho lăng trụ \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có đáy $A B C D$ là hình thoi cạnh \(a\), tâm \(O\) và \(ABC = {120^\circ }\). Các cạnh \({A^\prime }A;{A^\prime }B;{A^\prime }D\) cùng tạo với mặt đáy một góc bằng \({45^\circ }\). Tính theo \(a\) thề tích \(V\) của khối lăng trụ đã cho.
Trả lời bởi giáo viên
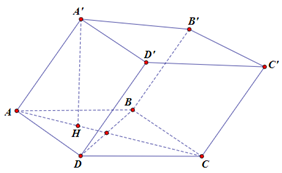
$A B C D$ là hình thoi cạnh \(a,\widehat {ABC} = {120^\circ }\)
\( \Rightarrow \Delta ABD\) đều cạnh do đó \({S_{ABCD}} = \dfrac{{{a^2}\sqrt 3 }}{2}.\)
Các cạnh \({A^\prime }A;\,\,{A^\prime }B;\,\,{A^\prime }D\) cùng tạo với mặt đáy một góc bằng \({45^\circ }\)
Nên chóp \({A^\prime }.ABD\) đều đỉnh \({A^\prime }\) suy ra \(AH = \dfrac{{a\sqrt 3 }}{3}\).
Suy ra \({V_{ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }}} = AH \cdot {S_{ABCD}} = \dfrac{{{a^3}}}{2}\).
Hướng dẫn giải:
Chứng minh chóp \({A^\prime }.ABD\) đều đỉnh \({A^\prime }\), từ đó tính được \(AH\).
\( \Rightarrow {V_{ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }}} = AH \cdot {S_{ABCD}}\)


