Cho khối nón đỉnh $S$ có bán kính đáy bằng $2\sqrt 3 a$. Gọi $A$ và $B$ là hai điểm thuộc đường tròn đáy sao cho $AB = 4a$. Biết khoảng cách từ tâm của đáy đến mặt phẳng $(SAB)$ bằng $2 a$, thể tích của khối nón đã cho bằng

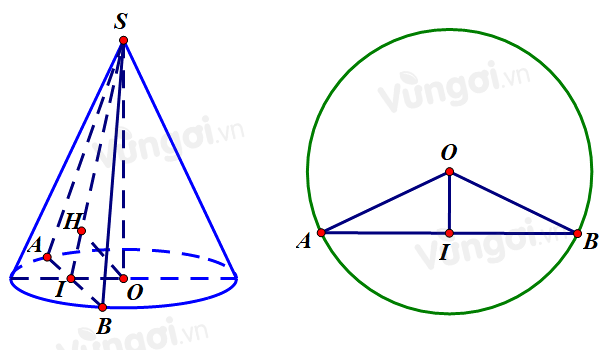
Ta có thể tích của khối nón là $V = \dfrac{1}{3}{S_d}.h = \dfrac{1}{2}\pi {r^2}h$

Có $r = 2\sqrt 3 a$. Ta cần tìm h=SO.

Gọi $I$ là trung điểm của $A B$.

Khi đó $\left\{ {\begin{array}{*{20}{l}}{SI \bot AB(\Delta SAB\text{ cân})}\\{OI \bot AB(\Delta OAB\text{ cân})}\end{array} \Rightarrow AB \bot (SOI)} \right.$

Mà $AB \subset (SAB) \Rightarrow (SAB) \bot (SOI)$

Kẻ $OH \bot SI$. Ta có: $\left\{ {\begin{array}{*{20}{l}}{(SAB) \bot (SOI)}\\{(SAB) \cap (SOI) = SI \Rightarrow OH \bot (SAB)}\\{OH \bot SI}\end{array}} \right.$

Suy ra $d(O,(SAB)) = OH = 2a$

Xét  vuông tại $I$ ta có:

$OI = \sqrt {O{A^2} - A{I^2}}  = \sqrt {O{A^2} - {{\left( {\dfrac{{AB}}{2}} \right)}^2}}$$= \sqrt {{{(2\sqrt 3 a)}^2} - {{\left( {\dfrac{{4a}}{2}} \right)}^2}}  = 2\sqrt 2 a$

Xét  vuông tại $S$ ta có:

$\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{I^2}}}$

$\Rightarrow \dfrac{1}{{S{O^2}}} = \dfrac{1}{{O{H^2}}} - \dfrac{1}{{O{I^2}}} = \dfrac{{O{I^2} - O{H^2}}}{{O{H^2} \cdot O{I^2}}}$

$\Rightarrow S{O^2} = \dfrac{{O{H^2} \cdot O{I^2}}}{{O{I^2} - O{H^2}}}$

$\Rightarrow SO = \dfrac{{OH \cdot OI}}{{\sqrt {O{I^2} - O{H^2}} }}$$= \dfrac{{2a \cdot 2\sqrt 2 a}}{{\sqrt {{{(2\sqrt 2 a)}^2} - {{(2a)}^2}} }} = 2\sqrt 2 a$

Vậy $V = \dfrac{1}{3}{S_d} \cdot h = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {(OA)^2}.SO$$= \dfrac{1}{3}\pi  \cdot {(2\sqrt 3 a)^2} \cdot 2\sqrt 2 a = 8\sqrt 2 \pi {a^3}$.