Cho hình vuông \(ABCD\) tâm \(O\) cạnh \(a\). Gọi \(M\) là trung điểm của \(AB\), \(N\) là điểm đối xứng với \(C\) qua $D$. Độ dài véc tơ \(\overrightarrow {MN} \) là:
Trả lời bởi giáo viên
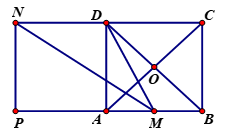
Qua $N$ kẻ đường thẳng song song với \(AD\) cắt \(AB\) tại \(P\).
Khi đó tứ giác \(ADNP\) là hình vuông và \(PM = PA + AM = a + \dfrac{a}{2} = \dfrac{{3a}}{2}\).
Áp dụng định lý Pitago trong tam giác vuông \(NPM\) ta có
\(M{N^2} = N{P^2} + P{M^2} = {a^2} + {\left( {\dfrac{{3a}}{2}} \right)^2} = \dfrac{{13{a^2}}}{4}\)\( \Rightarrow MN = \dfrac{{a\sqrt {13} }}{2}\)
Suy ra \(\left| {\overrightarrow {MN} } \right| = MN = \dfrac{{a\sqrt {13} }}{2}\).
Hướng dẫn giải:
Dựng tam giác vuông có chứa cạnh \(MN\) và sử dụng định lý Py-ta-go cho tam giác vuông để tính \(\left| {\overrightarrow {MN} } \right|\)

