Trả lời bởi giáo viên
Đáp án đúng: c
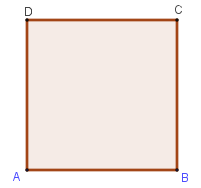
Phương án A: Do →DA.→CB=DA.CB.cos00=a2 nên loại A đúng, loại A.
Phương án B: Do →AB.→CD=AB.CD.cos180o=−a2 nên B đúng, loại B.
Phương án C: (→AB+→BC).→AC=→AC.→AC=AC2=(a√2)2=2a2 nên C sai, chọn C.
Phương án D: →AB.→AD+→CB.→CD=0 đúng vì AB⊥AD,CB⊥CD
Hướng dẫn giải:
Sử dụng công thức tính tích vô hướng của hai véc tơ: →a.→b=|→a||→b|.cos(→a,→b)

