Trả lời bởi giáo viên
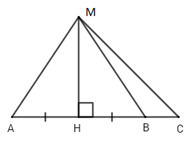
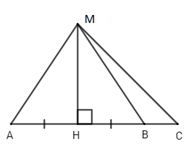
Vì $MH$ là đường vuông góc và $MA$ là đường xiên nên \(MA > MH\) (quan hệ đường vuông góc và đường xiên). Đáp án A đúng nên loại A.
Vì \(\widehat {MBC}\) là góc ngoài của \(\Delta MHB \Rightarrow \widehat {MBC} > \widehat {MHB} = {90^0}\)
Xét \(\Delta MBC\) có: \(\widehat {MBC}\) là góc tù nên suy ra \(MC > MB\) (quan hệ giữa góc và cạnh trong tam giác)
Mà $HB$ và $HC$ lần lượt là hình chiếu của $MB$ và $MC$ trên $AC.$
\( \Rightarrow HB < HC\) (quan hệ giữa đường xiên và hình chiếu). Đáp án B đúng nên loại đáp án B.
Vì \(AH = HB\left( {gt} \right)\) mà $AH$ và $HB$ lần lượt là hai hình chiếu của $AM$ và $BM.$
\( \Rightarrow MA = MB\) (quan hệ giữa đường xiên và hình chiếu). Đáp án C đúng nên loại đáp án C.
Ta có: \(\left\{ \begin{array}{l}MB = MA\left( {cmt} \right)\\MC > MB\left( {cmt} \right)\end{array} \right. \Rightarrow MC > MA\). Đáp án D sai nên chọn đáp án D.
Hướng dẫn giải:
Áp dụng các định lý sau:
- Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu.
- Quan hệ giữa góc và cạnh trong tam giác.