Câu hỏi:
3 năm trước
Cho hình thoi $ABCD$ có hai đường chéo $AC$ và $BD$ cắt nhau tại $O.$ Biết \(OA = 12cm\), diện tích hình thoi $ABCD$ là \(168c{m^2}\). Cạnh của hình thoi là:
Trả lời bởi giáo viên
Đáp án đúng: c
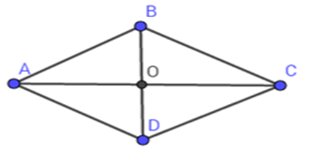
Ta có:
\(AC = 2AO = 2.12 = 24cm\)
\(\begin{array}{l}{S_{ABCD}} = \dfrac{1}{2}BD.AC \Rightarrow BD = \dfrac{{2{S_{ABCD}}}}{{AC}} = \dfrac{{2.168}}{{24}} = 14(cm)\\ \Rightarrow BO = \dfrac{1}{2}BD = \dfrac{1}{2}.14 = 7(cm)\end{array}\)
Áp dụng định lí Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
\(AB = \sqrt {A{O^2} + B{O^2}} = \sqrt {{{12}^2} + {7^2}} = \sqrt {193} (cm)\)
Hướng dẫn giải:
Tính $BO$, áp dụng định lí Py-ta-go trong tam giác vuông $AOB$ để tính cạnh $AB$

