Câu hỏi:
2 năm trước
Cho hình thang \(ABCD\)\(\left( {AB//CD} \right)\) có diện tích \(36\,c{m^2}\),\(AB = 4\,{\rm{cm,CD = 8}}\,{\rm{cm}}\). Gọi \(O\) là giao điểm của hai đường chéo. Tính diện tích tam giác \(COD\).
Trả lời bởi giáo viên
Đáp án đúng: c
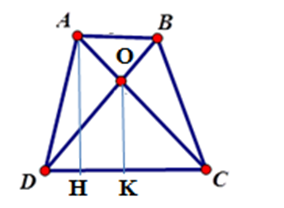
Kẻ \(AH \bot DC;\,OK \bot DC\) tại \(H;K\) suy ra \(AH{\rm{//}}OK\) .
Chiều cao của hình thang :\(AH = \dfrac{{2{S_{ABCD}}}}{{AB + CD}} = \dfrac{{2.36}}{{4 + 8}} = 6\left( {cm} \right)\)
Vì \(AB{\rm{//}}DC\) (do \(ABCD\) là hình thang) nên theo định lý Ta-lét ta có
\(\dfrac{{OC}}{{OA}} = \dfrac{{CD}}{{AB}} = \dfrac{8}{4} = 2\)\( \Rightarrow \dfrac{{OC}}{{OC + OA}} = \dfrac{2}{{2 + 1}} \Leftrightarrow \dfrac{{OC}}{{AC}} = \dfrac{2}{3}\)
Vì \(AH{\rm{//}}OK\) (cmt) nên theo định lý Ta-lét cho tam giác \(AHC\) ta có
\(\begin{array}{l}\dfrac{{OK}}{{AH}} = \dfrac{{OC}}{{AC}} = \dfrac{2}{3}\\ \Rightarrow OK = \dfrac{2}{3}AH \Leftrightarrow OK = \dfrac{2}{3}.6 = 4\,cm\end{array}\)
Do đó \({S_{COD}} = \dfrac{1}{2}OK.DC = \dfrac{1}{2}.4.8 = 16\left( {c{m^2}} \right)\).
Hướng dẫn giải:
Bước 1: Từ công thức tính diện tích hình thang ta tính chiều cao của hình thang.
Bước 2: Sử dụng định lý Ta-lét để tính chiều cao của tam giác \(ODC\) từ đó suy ra diện tích tam giác \(ODC\) .
