Câu hỏi:
2 năm trước
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y=\sqrt{x}\), \(y=-\,x\) và \(x=4.\) Thể tích của khối tròn xoay tạo thành khi quay hình \(\left( H \right)\) quanh trục hoành là \(V=\dfrac{a\pi }{b},\) với \(a,\,\,b>0\) và \(\dfrac{a}{b}\) là phân số tối giản. Tính tổng \(T=a+b.\)
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Đáp án:
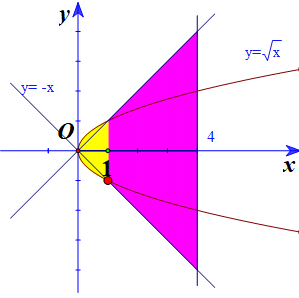
Hình trên là phần thiết diện của khối tròn xoay bị cắt bởi Oxy
Bước 1: Xét phương trình hoành độ giao điểm.
Phương trình hoành độ giao điểm của \(y=\sqrt{x},\,\,y=-\,x\) là \(\sqrt{x}=-\,x\Leftrightarrow x=0.\)
Bước 2: Tách tích phân ban đầu thành tích phân từ 0 đến 1 và từ 1 đến 4
Khi đó, thể tích cần tính là
\(\begin{array}{l}V = \pi \int\limits_0^1 {{{\left( {\sqrt x } \right)}^2}dx} + \pi \int\limits_1^4 {{{\left( { - x} \right)}^2}dx} \\ = \dfrac{\pi }{2} + 21\pi = \dfrac{{43\pi }}{2}\end{array}\)
=>$a+b=43+2=45$
Hướng dẫn giải:
Bước 1: Xét phương trình hoành độ giao điểm.
Bước 2: Tách tích phân ban đầu thành tích phân từ 0 đến 1 và từ 1 đến 4
