Câu hỏi:
2 năm trước
Cho hình lập phương ABCD.A′B′C′D′. Gọi φ là góc giữa hai mặt phẳng (A′BD) và (ABC). Tính tan2φ
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Đáp án:
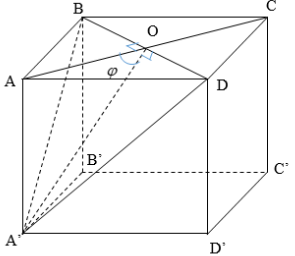
Gọi O là giao điểm của AC và BD. Vì ABCD là hình vuông nên AO⊥BD. Mặt khác AO là hình chiếu của A′O lên (ABCD) nên theo định lý 3 đường vuông góc ta có:
A′O⊥BD
⇒ Góc giữa (A′BD) và (ABC) là góc giữa AO và A′O và bằng ^A′OA
Giả sử cạnh của hình lập phương là a.
Tam giác A′OA vuông tại A nên có AA′=a,AO=a√22, tan^A′OA=AA′AO=aa√22=√2
⇒tan2φ=2
Hướng dẫn giải:
- Gọi O là giao điểm của AC và BD
- Sử dụng định lý 3 đường vuông góc


