Cho hình lăng trụ đứng \(ABC{\rm{D}}.A'B'C'D'\) có đáy là hình thang vuông ABCD vuông tại A, B \(\left( {A{\rm{D//}}BC} \right)\) và BC = 12 cm, AD = 16 cm, CD = 5 cm, đường cao ${\rm{AA}}' = 6\;cm$. Thể tích của hình lăng trụ là:

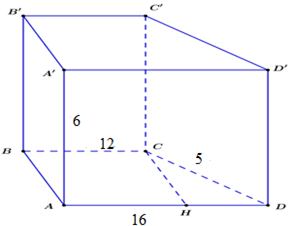
Trong mp $\left( {ABCD} \right)$ kẻ $CH$ vuông góc với $AD$ tại $H.$

Khi đó ta có $ABCH$ là hình chữ nhật. \(\left( {do\;\;\widehat A = \widehat B = \widehat H = 90^\circ } \right)\)

\( \Rightarrow BC = AH = 12\;cm \)\(\Rightarrow H{\rm{D}} = A{\rm{D}} - AH = 16 - 12 = 4\;cm\)

Xét tam giác $HCD$ vuông tại $H$ ta có:

\(H{C^2} + H{{\rm{D}}^2} = C{{\rm{D}}^2} \Leftrightarrow H{C^2} = C{{\rm{D}}^2} - H{{\rm{D}}^2} = {5^2} - {4^2} = 25 - 16 = 9 \Rightarrow HC = 3\;cm\)

Vậy thể tích của hình lăng trụ là:

$V{\rm{ }} = {\rm{ }}{S_{ABCD}}.h{\rm{ }} = {\rm{ }}{S_{ABCD}}.AA'$ \( = \dfrac{1}{2}AA'.\left( {BC + AD} \right).CH = \dfrac{1}{2}.3.(12 + 16).6 = 252\;c{m^3}\) \(\)