Câu hỏi:
2 năm trước
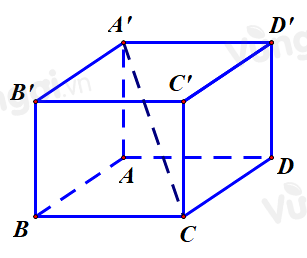
Cho hình hộp chữ nhật \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có \(AB = AD = 2\) và \(A{A^\prime } = 2\sqrt 2 \) (tham khảo hình bên). Góc giữa đường thẳng \(C{A^\prime }\) và mặt phẳng \((ABCD)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có AA’ vuông góc với (ABCD) nên A là hình chiếu của A’ trên (ABCD)
=> CA là hình chiếu của CA’ lên (ABCD)
=> Góc cần tìm là \(\widehat {A'CA} = \alpha \).
Vì đáy là hình vuông nên \(AC = AB\sqrt 2 = 2\sqrt 2 \) và \(\tan \alpha = \dfrac{{A{A^\prime }}}{{AC}} = 1 \Rightarrow \alpha = {45^o}\)
Hướng dẫn giải:
- Xác định góc giữa đường thẳng \(C{A^\prime }\) và mặt phẳng \((ABCD)\)
- Tính góc.
