Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O$ và có $AC = a, BD = b. $ Tam giác $SBD$ là tam giác đều. Một mặt phẳng $(P)$ di động song song với $(SBD)$ đi qua $I$ trên đoạn $OC.$ Đặt \(AI = x\,\,\left( {\dfrac{a}{2} < x < a} \right)\). Khi đó diện tích thiết diện của hình chóp với mặt phẳng $(P)$ là:
Trả lời bởi giáo viên
Đáp án đúng: c
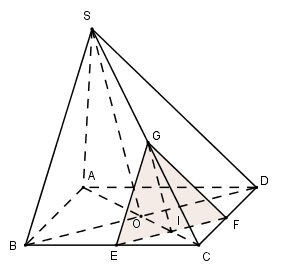
Trong $(ABCD)$ qua $I$ kẻ $EF // BD$ \(\left( {E \in BC;F \in CD} \right)\)
Trong $(SAC)$ qua $I$ kẻ $IG // SO$ \(\left( {G \in SC} \right)\)
\( \Rightarrow \left( {GEF} \right)\) qua $I$ và song song với $(SBD)$ \( \Rightarrow \left( P \right) \equiv \left( {GEF} \right)\)
Ta có: \(\left\{ \begin{array}{l}\left( {GEF} \right) \cap \left( {SBC} \right) = GE\\\left( {SBD} \right) \cap \left( {SBC} \right) = SB\\\left( {GEF} \right)//\left( {SBD} \right)\end{array} \right. \Rightarrow GE//SB\)
Tương tự ta chứng minh được $GF // SD.$
Ta có:
\(\left\{ \begin{array}{l}\dfrac{{IC}}{{OC}} = \dfrac{{FE}}{{BD}} = \dfrac{{GC}}{{SC}} = \dfrac{{GE}}{{SB}} = \dfrac{{GF}}{{SD}}\\BD = SB = SD\end{array} \right. \Rightarrow GE = GF = EF \Rightarrow \Delta GEF\) đều và \(\dfrac{{IC}}{{OC}} = \dfrac{{EF}}{{BD}}\) \( \Rightarrow EF = \dfrac{{IC}}{{OC}}.BD = \dfrac{{a - x}}{{\frac{a}{2}}}.b = \dfrac{{2b\left( {a - x} \right)}}{a}\)
\( \Rightarrow \Delta GEF\) đều cạnh \(\dfrac{{2(a - x)}}{a}.b\) , do đó \({S_{\Delta GEF}} = \dfrac{{{{\left( {\dfrac{{2(a - x)}}{a}} \right)}^2}.{b^2}\sqrt 3 }}{2} = \dfrac{{{b^2}{{\left( {a - x} \right)}^2}\sqrt 3 }}{{{a^2}}}\)
Hướng dẫn giải:
Dựng mặt phẳng qua $I$ và song song với $(SBD),$ dựng thiết diện.
Chứng minh thiết diện là tam giác đều và tính diện tích tam giác đều đó.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 7: Quan hệ song song trong không gian - đề số 2 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: Quan hệ song song trong không gian - đề số 3 Toán 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 7: Quan hệ song song trong không gian - đề số 2 Toán 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 7: Quan hệ song song trong không gian - đề số 3 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: Quan hệ song song trong không gian - đề số 1 Toán 11 có lời giải chi tiết
