Câu hỏi:
3 năm trước
Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O.$ Lấy điểm $I$ trên đoạn $SO$ sao cho \(\dfrac{{SI}}{{SO}} = \dfrac{2}{3}\), $BI$ cắt $SD$ tại $M$ và $DI$ cắt $SB$ tại $N. $ Khi đó $MNBD$ là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: a
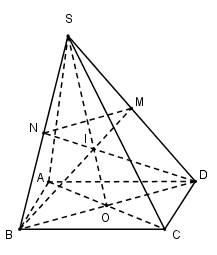
Dễ thấy $I$ là trọng tâm của tam giác $SBD $ nên $BI, DI$ là các đường trung tuyến của tam giác $SBD.$
Suy ra $M, N$ lần lượt là trung điểm của $SD$ và $SB.$
Nên $MN$ là đường trung bình của tam giác $SBD$ \( \Rightarrow \) $MN // BD.$
Vậy tứ giác $MNBD $ là hình thang.
Hướng dẫn giải:
- Sử dụng các tính chất của trọng tâm tam giác.
- Sử dụng tính chất đường trung bình của tam giác.
- Sử dụng định nghĩa hai đường thẳng song song.

