Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,\,AD = 2a\), \(SA \bot \left( {ABCD} \right)\) và \(SA = 2a\). Tính thể tích khối cầu ngoại tiếp hình chóp \(S.ABCD\).

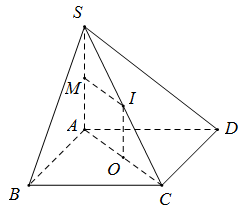
Gọi $O$ là tâm hình chữ nhật $ABCD,M$ và $I$ lần lượt là trung điểm $SA,SC \Rightarrow AOIM$ là hình chữ nhật.

Ta có $O$ là tâm đường tròn ngoại tiếp hình chữ nhật $ABCD,OI \bot \left( {ABCD} \right)$ nên $OI$ là trục đường tròn ngoại tiếp hình chữ nhật $ABCD$

$IM \bot SA \Rightarrow IM$ là trung trực $SA$ trong mặt phẳng $\left( {SAC} \right)$

$ \Rightarrow I$ là tâm mặt cầu ngoại tiếp hình chóp.

Có $OI = AM = \dfrac{{SA}}{2} = a;OC = \dfrac{{AC}}{2} = \dfrac{1}{2}\sqrt {A{B^2} + A{D^2}}  = \dfrac{{a\sqrt 5 }}{2}$

Bán kính và thể tích mặt cầu lần lượt là

$\begin{array}{l}R = IC = \sqrt {I{O^2} + O{C^2}}  = \dfrac{{3a}}{2}\\V = \dfrac{4}{3}\pi {R^3} = \dfrac{{9\pi {a^3}}}{2}\end{array}$