Câu hỏi:
2 năm trước
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Tam giác SBD đều. Một mặt phẳng (P) song song với (SBD) và đi qua điểm I thuộc cạnh AC (không trùng với A hoặc C). Thiết diện của (P) với hình chóp là hình gì ?
Trả lời bởi giáo viên
Đáp án đúng: d
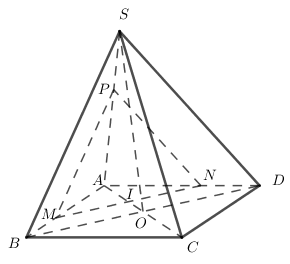
Trong $(ABCD)$ qua $I$ kẻ $MN // BD $ \(\left( {M \in AB;N \in AD} \right)\)
Trong $(SAB)$ qua $M$ kẻ $MP // SB$ \(\left( {P \in SA} \right)\)
\( \Rightarrow \left( {MNP} \right)//\left( {SBD} \right) \Rightarrow \left( P \right) \equiv \left( {MNP} \right)\)
\(\left\{ \begin{array}{l}\left( {MNP} \right) \cap \left( {SAD} \right) = NP\\\left( {SBD} \right) \cap \left( {SAD} \right) = SD\\\left( {MNP} \right)//\left( {SBD} \right)\end{array} \right. \Rightarrow NP//SD\)
Theo định lí Ta-let ta có: \(\dfrac{{MN}}{{BD}} = \dfrac{{AM}}{{AB}} = \dfrac{{AP}}{{AS}} = \dfrac{{MP}}{{SB}} = \dfrac{{NP}}{{SD}}\)
Mà tam giác \(SBD\) đều nên \(SB = BD = SD \Rightarrow MN = NP = MP\)
Vậy \(\Delta MNP\) đều.
Hướng dẫn giải:
Dựng thiết diện bằng cách kẻ các đường thẳng song song.
Sử dụng định lí Ta-let.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 7: Quan hệ song song trong không gian - đề số 2 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: Quan hệ song song trong không gian - đề số 3 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: Quan hệ song song trong không gian - đề số 1 Toán 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 7: Quan hệ song song trong không gian - đề số 2 Toán 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 7: Quan hệ song song trong không gian - đề số 3 Toán 11 có lời giải chi tiết
