Câu hỏi:
2 năm trước
Cho hình bình hành ABCD. Gọi Bx,Cy,Dz là các đường thẳng song song với nhau lần lượt đi qua B,C,D và nằm về một phía của mặt phẳng (ABCD), đồng thời không nằm trong mặt phẳng (ABCD). Một mặt phẳng đi qua A và cắt Bx,Cy,Dz lần lượt tại các điểm B′,C′,D′ với BB′=2,DD′=4. Khi đó CC′ bằng:
Trả lời bởi giáo viên
Đáp án đúng: d
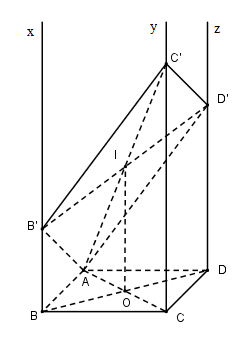
Trên Bx và Dz lấy điểm B′ và D′ sao cho BB′=2,DD′=4.
Gọi O là tâm hình bình hành ABCD,I là trung điểm của B′D′
Ta có BDD′B′ là hình thang, OI là đường trung bình của hình thang nên OI//BB′//DD′//Cy và OI=BB′+DD′2=2+42=3.
Xét mặt phẳng tạo bởi OI và CC′ có: AI∩Cy=C′.
Ta có OI//CC′,AO=OC suy ra AI=IC′
Suy ra OI là đường trung bình của tam giác ACC′ ⇒CC′=2OI=6
Hướng dẫn giải:
- Đưa về cùng mặt phẳng;
- Sử dụng các tính chất của đường trung bình của tam giác, đường trung bình của hình thang.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 7: Quan hệ song song trong không gian - đề số 3 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: Quan hệ song song trong không gian - đề số 2 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: Quan hệ song song trong không gian - đề số 1 Toán 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 7: Quan hệ song song trong không gian - đề số 2 Toán 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 7: Quan hệ song song trong không gian - đề số 3 Toán 11 có lời giải chi tiết
