Câu hỏi:
2 năm trước
Cho hình chóp $S.ABC$ có $SA \bot (ABC);AC = b,AB = c,\widehat {BAC} = \alpha $. Gọi $B',C'$ lần lượt là hình chiếu vuông góc của $A$ lên $SB,SC$. Tính bán kính mặt cầu ngoại tiếp khối chóp $A.{\rm{ }}BCC'B'$ theo $b,c,\alpha $
Trả lời bởi giáo viên
Đáp án đúng: c
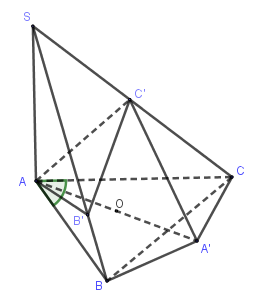
Gọi $AA'$ là đường kính của đường tròn ngoại tiếp tam giác $ABC$
\(AC \bot A'C;\,AB \bot A'B\)
Ta chứng minh \(AC' \bot A'C'\)
\(SA \bot A'C;\,AC \bot A'C \Rightarrow A'C \bot AC'\)
Mà \(AC' \bot SC \Rightarrow AC' \bot A'C'\)
Tương tự \(AB' \bot A'B'\)
Như vậy $B,C,C',B'$ cùng nhìn $AA'$ bằng $1$ góc vuông nên $A,B,C,B',C'$ cùng thuộc $1$ mặt cầu có đường kính là $AA'$ và cũng đồng thời là đường kính của đường tròn ngoại tiếp tam giác $ABC$.
Tính \(BC = \sqrt {{b^2} + {c^2} - 2b\cos \alpha } \)
Trong tam giác \(ABC:\dfrac{{BC}}{{\sin A}} = 2R \Rightarrow R = \dfrac{{\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } }}{{2\sin \alpha }}\)
Hướng dẫn giải:
+ Chứng minh được tâm mặt cầu ngoại tiếp của hình chóp $ABCC'B'$ trùng với tâm đường tròn ngoại tiếp của tam giác
