Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên hợp với đáy một góc bằng 60∘. Kí hiệu V1,V2 lần lượt là thể tích khối cầu ngoại tiếp, thể tích khối nón ngoại tiếp hình chóp đã cho. Tính tỉ số V1V2.
Trả lời bởi giáo viên
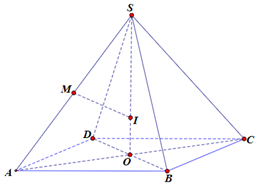
Gọi O là tâm hình vuông ABCD⇒SO⊥(ABCD).
Khi đó góc giữa cạnh bên SA với mặt đáy (ABCD) là góc ^SAO.
Theo giả thiết: ^SAO=60∘ nên tam giác SAC đều.
Suy ra SA=a√2 và SO=a√62.
Gọi M là trung điểm SA.
Trong (SAC), đường trung trực của cạnh SA cắt SO tại I.
Khi đó, IS=IA=IB=IC=ID nên I là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD.
Tam giác SAO có SI.SO=SM.SA⇒SI=SA22SO=a√63=R.
Ta lại có, khối nón ngoại tiếp hình chóp có đường tròn đáy ngoại tiếp hình vuông ABCD nên có:
Bán kính đáy r=a√22 và chiều cao h=SO=a√62.
Suy ra: V1V2=43⋅π(a√63)313π(a√22)2⋅a√62=329.
Hướng dẫn giải:
Công thức tính thể tích khối cầu: V=43πR3.
Công thức tính thể tích khối nón: V=13πR2h.


