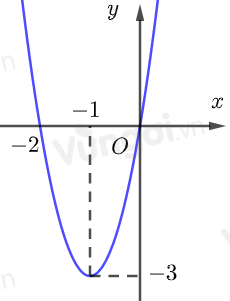
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ. Phương trình \(f\left( {f\left( x \right)} \right) = - 2\) có tất cả bao nhiêu nghiệm thực phân biệt?
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
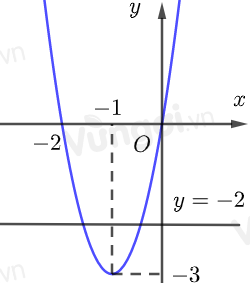
Từ đồ thị ta có:
\(f\left( {f\left( x \right)} \right) = - 2 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = {a_1} \in \left( { - 2; - 1} \right)\\f\left( x \right) = {a_2} \in \left( { - 1;0} \right)\end{array} \right.\)
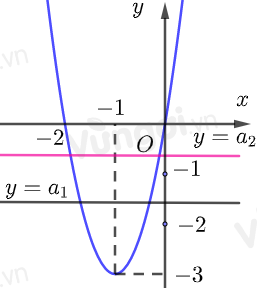
Với \(f\left( x \right) = {a_1} \in \left( { - 2; - 1} \right)\) thì đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = {a_1}\) tại 2 điểm nên \(f\left( x \right) = {a_1}\)có 2 nghiệm
Với \(f\left( x \right) = {a_2} \in \left( { - 1;0} \right)\) thì đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = {a_2}\) tại 2 điểm nên \(f\left( x \right) = {a_2}\) có 2 nghiệm
Vậy phương trình đã cho có 4 nghiệm phân biệt.
Hướng dẫn giải:
- Tìm nghiệm \(f\left( x \right)\) của phương trình \(f\left( {f\left( x \right)} \right) = - 2\)
- Tìm số nghiệm của phương trình \(f\left( x \right) = m\)


