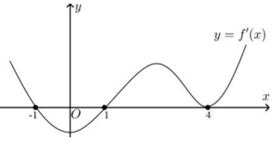
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị \(y = f'\left( x \right)\) có đồ thị như hình dưới. hỏi hàm số \(g\left( x \right) = f\left( {1 - {x^2}} \right)\) giảm trên khoảng nào sau đây?
Trả lời bởi giáo viên
Ta có:
\(\begin{array}{l}g'\left( x \right) = f'\left( {1 - {x^2}} \right)\left( { - 2x} \right)\\g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f'\left( {1 - {x^2}} \right) = 0\\\left( { - 2x} \right) = 0\end{array} \right.\end{array}\)
\(f'\left( {1 - {x^2}} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}1 - {x^2} = - 1\\1 - {x^2} = 1\\1 - {x^2} = 4\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = \pm \sqrt 2 \\x = 0\\x \in \emptyset \end{array} \right.\)
\(f'\left( {1 - {x^2}} \right) < 0 \Leftrightarrow - 1 < 1 - {x^2} < 1\)
\( \Leftrightarrow - \sqrt 2 < x < \sqrt 2 \)
Bảng biến thiên:
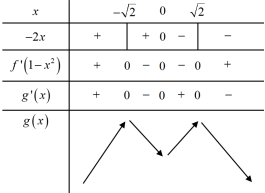
Từ bảng biến thiên ta thấy hàm số giảm trên \(\left( { - 1;0} \right)\)
Hướng dẫn giải:
- Tính $g’(x)$ và giải \(g'\left( x \right) = 0\)
- Lập bảng biến thiên


