Câu hỏi:
2 năm trước
Cho hàm số f(x) có đồ thị trên đoạn [−3;3] là đường gấp khúc ABCD như hình vẽ.
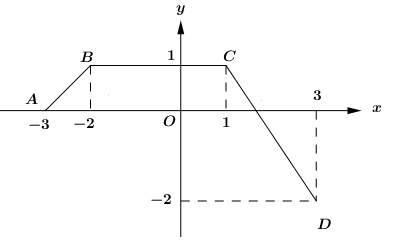
Tính 3∫−3f(x)dx.
Trả lời bởi giáo viên
Đáp án đúng: a
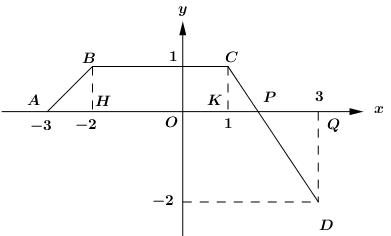
Ta có:
3∫−3f(x)dx=SABH+SBCKH+SCPK−SDPQ=12.1.1+3.1+12.1.23−12.43.2=52.
Hướng dẫn giải:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox trên [−3;3].

