Cho hàm số \(f\left( x \right)\) có đồ thị \(f'\left( x \right)\) như hình vẽ dưới. hàm số \(g\left( x \right) = f\left( x \right) - \dfrac{{{x^3}}}{3} + 2{x^2} - 5x + 2022\) có bao nhiêu điểm cực trị?
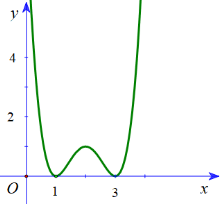
Chỉ được điền các số nguyên, phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Có
\(\begin{array}{l}g'\left( x \right) = f'\left( x \right) - {x^2} + 4x - 5\\g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = {x^2} - 4x + 5\end{array}\)
Ta có đồ thị hàm số \(y = {x^2} - 4x + 5\) và đồ thị hàm \(y = f'\left( x \right)\) như hình vẽ dưới
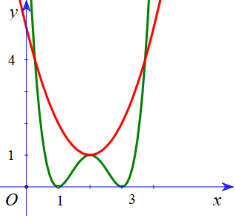
Quan sát hình vẽ ta thấy \(g'\left( x \right) = 0\) có 3 nghiệm phân biệt trong đó chỉ có 1 nghiệm bội chẵn.
Vậy hàm số \(g\left( x \right)\) có 2 điểm cực trị.
Hướng dẫn giải:
- Tính \(g'\left( x \right)\)
- Vẽ thêm đồ thị hàm số \(y = {x^2} - 4x + 5\) vào đồ thị \(y = f'\left( x \right)\)
- Hoành độ của tiếp điểm 2 đồ thị là nghiệm bội của phương trình tạo bởi hai đồ thị đó.
- Tìm số điểm mà hai đồ thị cắt nhau nhưng không tiếp xúc.


