Cho hàm số \(f\left( x \right) = \dfrac{{ax - 1}}{{bx + c}}\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:

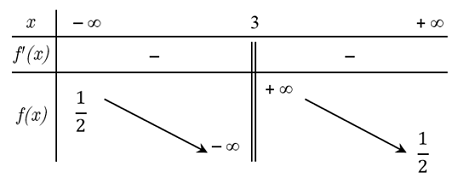
Khẳng định nào dưới đây đúng?

TXĐ: \(D = \mathbb{R}\backslash \left\{ 3 \right\}\).

Dựa vào BBT, ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to  \pm \infty } f\left( x \right) = \dfrac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) =  + \infty ,\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) =  - \infty \end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{a}{b} = \dfrac{1}{2}\\ - \dfrac{c}{b} = 3\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}a = \dfrac{b}{2}\\c =  - 3b\end{array} \right.\)

Ta có: \(f\left( x \right) = \dfrac{{ax - 1}}{{bx + c}}\, \Rightarrow f'\left( x \right) = \dfrac{{ac + b}}{{{{\left( {bx + c} \right)}^2}}}\).

Dựa vào BBT ta thấy \(f'\left( x \right) < 0\,\,\,\forall x \ne 3 \Leftrightarrow ac + b < 0\,\,\forall x \ne 3\)\( \Leftrightarrow \dfrac{b}{2}.\left( { - 3b} \right) + b < 0 \Leftrightarrow \left[ \begin{array}{l}b < 0\\b > \dfrac{2}{3}\end{array} \right.\).