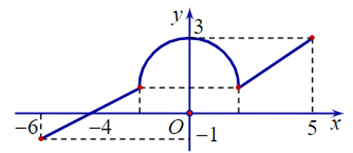
Cho hàm số \(f\) liên tục trên đoạn \([ - 6;5]\), có đồ thị gồm hai đoạn thẳng và nửa đường tròn như hình vẽ. Tính giá trị \(I = \int\limits_{ - 6}^5 {\left[ {f\left( x \right) + 2} \right]} dx\)
Trả lời bởi giáo viên
\(f(x) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{1}{2}x + 2\quad {\rm{ khi }} - 6 \le x \le - 2}\\{1 + \sqrt {4 - {x^2}} }\\{\dfrac{2}{3}x - \dfrac{1}{3}\quad {\rm{khi}} - 2 \le x \le 2}\end{array}{\rm{ khi }}2 \le x \le 5} \right.\)
Ta có:
\(I = \int\limits_{ - 6}^5 {\left[ {f\left( x \right) + 2} \right]} dx = \int\limits_{ - 6}^5 {f\left( x \right)dx + } 2\int\limits_{ - 6}^5 {dx} \)
\( = \int_{ - 6}^{ - 2} {\left( {\dfrac{1}{2}x + 2} \right)} {\rm{d}}x + \int_{ - 2}^2 {\left( {1 + \sqrt {4 - {x^2}} } \right)} {\rm{d}}x + \int_2^5 {\left( {\dfrac{2}{3}x - \dfrac{1}{3}} \right)} {\rm{d}}x + 22\)
\( = \left. {\left( {\dfrac{1}{4}{x^2} + 2x} \right)} \right|_{ - 6}^{ - 2} + J + \left. {\left( {\dfrac{1}{3}{x^2} - \dfrac{x}{3}} \right)} \right|_2^5 + 22 = J + 28.\)
Tính \(J = \int_{ - 2}^2 {\left( {1 + \sqrt {4 - {x^2}} } \right)} {\rm{d}}x\)
Đặt \({\rm{ }}x = 2\sin t \Rightarrow {\rm{d}}x = 2\cos t\;{\rm{d}}t.\)
Đổi cận: Khi \(\,x = -2\) thì \(t = - \dfrac{\pi }{2};\) khi Khi \(\,x = 2\) thì \(t = \dfrac{\pi }{2};\)
\(J = \int_{ - 2}^2 {\left( {1 + \sqrt {4 - {x^2}} } \right)} {\rm{d}}x = 4 + 4\int\limits_{ - \dfrac{\pi }{2}}^{\dfrac{\pi }{2}} {{{\cos }^2}t\,dt} = 4 + 2\int\limits_{ - \dfrac{\pi }{2}}^{\dfrac{\pi }{2}} {(1 + \cos 2t)dt} = 4 + 2\pi {\rm{. }}\)
Vậy \(I = 32 + 2\pi {\rm{.}}\)
Hướng dẫn giải:
- Xác định hàm f(x)
- Sử dụng phương pháp đổi biến \({\rm{ }}x = 2\sin t\).
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
