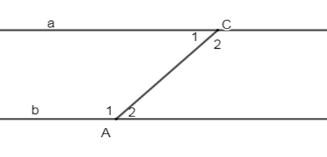
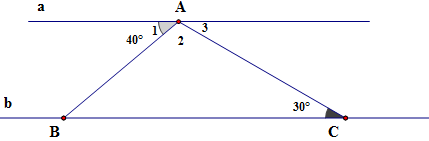
Cho hai đường thẳng $a,{\rm{ }}b$ song song. Điểm $A\; \in \;a,{\rm{ }}B\; \in \;b,{\rm{ }}C\; \in \;b.\;$
Biết $\widehat {BAa} = {40^0},\widehat {ACB} = {30^0}$  như hình vẽ. Câu nào sau đây đúng?

$\left| x \right| = x$

$\left| x \right| =  - x$

$\left| x \right| < 0$

$\left| x \right| = 0$

$1$

$2$

$3$

$4$

\(\widehat {{A_2}} = 80^\circ ;\,\widehat {{C_2}} = 110^\circ \)

\(\widehat {{A_2}} = 110^\circ ;\,\widehat {{C_2}} = 70^\circ \)                          

\(\widehat {{A_2}} = 70^\circ ;\,\widehat {{C_2}} = 110^\circ \)

\(\widehat {{A_2}} = 70^\circ ;\,\widehat {{C_2}} = 70^\circ \)

\(x//\,y\) vì có hai góc đồng vị bằng nhau                  

\(x//\,y\) vì có hai góc so le trong bằng nhau 

\(x//\,y\) vì có hai góc trong cùng phía bằng nhau

\(x//\,y\) vì có hai góc so le ngoài bằng nhau

\(\widehat {MEF} = 133^\circ \)       

\(\widehat {MEI} = 47^\circ \)          

\(\widehat {IEN} = 133^\circ \)

Cả A, B, C đều đúng.

\(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x + y}}{{a + b}}\)

\(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x.y}}{{a.b}}\)

\(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x.y}}{{a + b}}\)

\(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x - y}}{{a + b}}\)

${a^m}.{a^n} = {a^{m + n}}$

${\left( {a.b} \right)^m} = {a^m}.{b^m}$

\({\left( {{a^m}} \right)^n} = {a^{m + n}}\)

${\left( {{a^m}} \right)^n} = {a^{m.n}}$