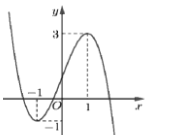
Cho \(f\left( x \right) = {\left( {x - 1} \right)^3} - 3x + 3\). Đồ thị hình bên là của hàm số có công thức:
Trả lời bởi giáo viên
Đáp án A: \(y = - f\left( {x + 1} \right) - 1 = - {x^3} - 3\left( {x + 1} \right) + 3 - 1 = - {x^3} - 3x - 1\). Đồ thị hàm số đi qua điểm \(\left( {0; - 1} \right) \Rightarrow \) Loại.
Đáp án B: \(y = - f\left( {x + 1} \right) + 1 = - {x^3} - 3\left( {x + 1} \right) + 3 + 1 = - {x^3} + 3x + 1\). Đồ thị hàm số đi qua điểm \(\left( {0;1} \right) \Rightarrow \) Đáp án B có thể đúng.
Đáp án C: \(y = - {\left( {x - 2} \right)^3} - 3\left( {x - 1} \right) - 1 = - {x^3} + 6{x^2} - 15x + 10 = 0\). Đồ thị hàm số đi qua điểm \(\left( {0;10} \right) \Rightarrow \) Loại.
Đáp án D: \(y = - {\left( {x - 2} \right)^3} - 3\left( {x - 1} \right) + 1 = - {x^3} + 6{x^2} - 15x + 12 = 0\). Đồ thị hàm số đi qua điểm \(\left( {0;12} \right) \Rightarrow \) Loại.
Hướng dẫn giải:
Xác định các hàm số ở các đáp án, thử điểm mà đồ thị hàm số đi qua để loại đáp án.


