Câu hỏi:
2 năm trước
Cho đường tròn $\left( {O;R} \right)$ có hai dây $AB,CD$ vuông góc với nhau ở $M$. Biết $AB = 14\,cm;\,CD = 12\,cm;\,MC = 2\,cm.$ Bán kính $R$ và khoảng cách từ tâm $O$ đến dây $CD$ lần lượt là
Trả lời bởi giáo viên
Đáp án đúng: b
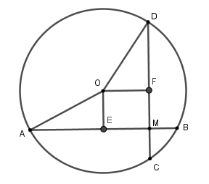
Lấy $E$; $F$ lần lượt là trung điểm của hai dây $AB$ và $CD$. Khi đó
\(OE \bot AB;\,OF \bot AC\) lại có \(\widehat {FME} = 90^\circ \) nên \(OEMF\) là hình chữ nhật. Suy ra $OE=MF=CF-MC=4 \,\ cm.$
Xét đường tròn tâm $\left( O \right)$,
Có $OE = \,4\,cm$, $E$ là trung điểm của $AB$ nên $AE = \dfrac{{14}}{2} = 7cm$
Áp dụng định lý Pytago cho tam giác vuông $OEA$ ta có $OA = \sqrt {A{E^2} + O{E^2}} = \sqrt {65} $ nên $R = \sqrt {65} $
Lại có $OD = \sqrt {65} \,\ cm ;FD = 6 \,\ cm$ nên áp dụng định lý Pytago cho tam giác vuông $OFD$ ta có
$OF = \sqrt {O{D^2} - F{D^2}} = \sqrt {29} \,\ cm$. Do đó khoảng cách từ tâm đến dây $CD$ là $\sqrt {29} $$cm$ .
Hướng dẫn giải:
Kẻ các đường vuông góc từ tâm đến dây. Sử dụng mối liên hệ giữa dây và đường kính và tính chất hình chữ nhật để suy ra khoảng cách.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 6: đường tròn - đề số 2 Toán 9 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 6: đường tròn - đề số 1 Toán 9 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 6: đường tròn - đề số 2 Toán 9 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 6: đường tròn - đề số 1 Toán 9 có lời giải chi tiết
