Câu hỏi:
2 năm trước
Cho đường tròn \(\left( O \right)\) đường kính \(AB,\) vẽ góc ở tâm \(\widehat {AOC} = 55^\circ \) . Vẽ dây \(CD\) vuông góc với \(AB\) và dây \(DE\) song song với \(AB.\) Tính số đo cung nhỏ \(BE\)
Trả lời bởi giáo viên
Đáp án đúng: a
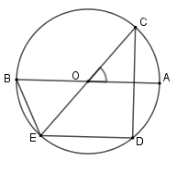
Xét $\left( O \right)$ có $CD \bot OA;ED{\rm{//}}OA \Rightarrow CD \bot ED$ hay $\widehat {EDC} = 90^\circ $ mà $E;D;C \in \left( O \right)$ nên $EC$ là đường kính của $\left( O \right)$ hay $E;O;C$ thẳng hàng.
Do đó $\widehat {BOE} = \widehat {COA} = 55^\circ $ (đối đỉnh) nên số đo cung nhỏ $BE$ là $55^\circ $.
Hướng dẫn giải:
Bước 1: Chứng minh $E;O;C$ thẳng hàng
Bước 2: Tính số đo cung thông qua góc ở tâm

